Skip to main content

一位未曾涉足算法的初学者收获

· 10 min read
Kuizuo

正如标题所言，在我四年的编程经历中就没刷过一道算法题，这可能与我所编写的应用有关，算法对我而言提升不是特别大。加上我几乎都是在需求中学习，而非系统性的学习。所以像算法这种基础知识我自然就不是很熟悉。

那我为何会接触算法呢？​

我在今年暑假期间有一个面试，当时面试官想考察下我的算法能力，而我直接明摆了说我不行（指算法上的不行），但面试官还是想继续考察，于是就出了道斐波那契数列作为考题。

但我毕竟也接触了 4 年的代码，虽说不刷算法，但起码也看过许多文章和代码，斐波那契数列使用递归实现的代码也有印象，于是很快我就写出了下面的代码作为我的答案。

function fib(n) {
  if (n <= 1) return n

  return fib(n - 1) + fib(n - 2)
}

面试官问我还有没有更好的答案，我便摇了摇头表示这 5 行不到的代码难道不是最优解？

事实上这份代码看起来很简洁，实际却是耗时最慢的解法

毫无疑问，在算法这关我肯定是挂了的，不过好在项目经验及后续的项目实践考核较为顺利，不然结局就是回去等通知了。最后面试接近尾声时，面试官友情提醒我加强基础知识（算法），强调各种应用框架不断更新迭代，但计算机的底层基础知识是不变的。于是在面试官的建议下，便有了本文。

好吧，我承认我是为了面试才去学算法的。

对上述代码进行优化​

在介绍我是从何处学习算法以及从中学到了什么，不妨先来看看上题的最优答案是什么。

对于有接触过算法的同学而言，不难看出时间复杂度为 O(n²)，而指数阶属于爆炸式增长，当 n 非常大时执行效果缓慢，且可能会出现函数调用堆栈溢出。

如果仔细观察一下，会发现这其中进行了非常多的重复计算，我们不妨将设置一个 res 变量来输出一下结果

function fib(n) {
  if (n <= 1) {
    return n
  }

  const res = fib(n - 1) + fib(n - 2)
  console.log(res)
  return res
}

当 n=7 时，所输出的结果如下

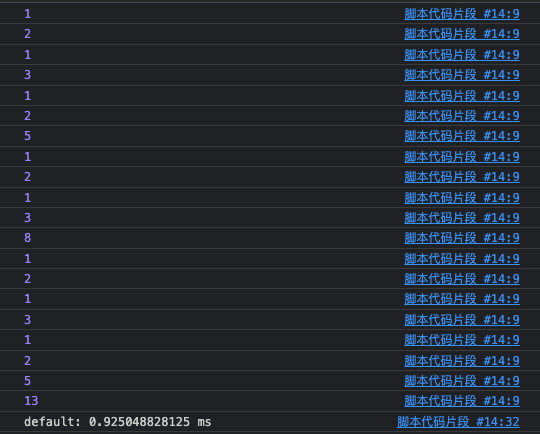
Untitled

这还只是在 n=7 的情况下，便有这么多输出结果。而在算法中要避免的就是重复计算，这能够高效的节省执行时间，因此不妨定义一个缓存变量，在递归时将缓存变量也传递进去，如果缓存变量中存在则说明已计算过，直接返回计算结果即可。

function fib(n, mem = []) {
  if (n <= 1) {
    return n
  }

  if (mem[n]) {
    return mem[n]
  }

  const res = fib(n - 1, mem) + fib(n - 2, mem)
  console.log(res)
  mem[n] = res
  return res
}

此时所输出的结果可以很明显的发现没有过多的重复计算，执行时间也有显著降低。

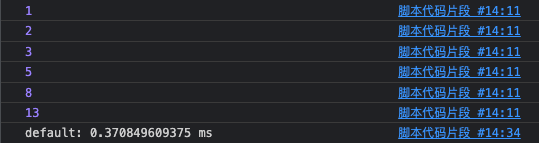
Untitled

这便是记忆化搜索，时间复杂度被优化至 O(n)。

可这还是免不了递归调用出现堆栈溢出的情况（如 n=10000 时）。

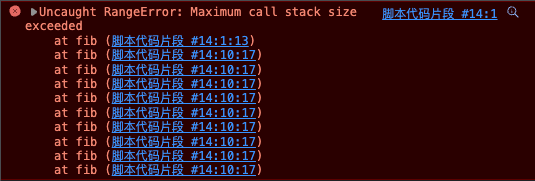
Untitled

从上面的解法来看，都是从”从顶至底”，比方说 n=7，会先求得 n=6 的结果, 而 n=6 又要求得 n=5 的结果，依次类推直至得到底层 n=1 的结果。

事实上我们可以换一种思路，先求得 n=1，n=2 的结果，然后依次类推上去，最终得到 n=6，n=7 的结果，也就是“从底至顶”，而这就是动态规划的方法。

从代码上来分析，因此我们可以初始化一个 dp 数组，用于存放数据状态。

function fib(n) {
  const dp = [0, 1]

  for (let i = 2; i <= n; i++) {
    dp[i] = dp[i - 1] + dp[i - 2]
  }

  return dp[n]
}

最终 dp 数组的最后一个成员便是原问题的解。此时输出 dp 数组结果。

Untitled

且由于不存在递归调用，因此你当 n=10000 时也不在会出现堆栈溢出的情况（只不过最终的结果必定超出了 JS 数值可表示范围，所以只会输出 Infinity）

对于上述代码而言，在空间复杂度上能够从 O(n) 优化到 O(1)，至于实现可以参考 空间优化，这里便不再赘述。

我想至少从这里你就能看出算法的魅力所在，这里我强烈推荐 hello-algo 这本数据结构与算法入门书，我的算法之旅的起点便是从这本书开始，同时激发起我对算法的兴趣。

两数之和​

于是在看完了这本算法书后，我便打开了大名鼎鼎的刷题网站 LeetCode，同时打开了究极经典题目的两数之和。

有人相爱，有人夜里开车看海，有人 leetcode 第一题都做不出来。

题干：

给定一个整数数组 nums  和一个整数目标值 target，请你在该数组中找出和为目标值 target 的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

以下代码将会采用 JavaScript 代码作为演示。

暴力枚举​

我初次接触该题也只会暴力解法，遇事不决，暴力解决。也很验证了那句话：不论多久过去，我首先还是想到两个 for。

var twoSum = function (nums, target) {
  const n = nums.length

  for (let i = 0; i < n; i++) {
    for (let j = 0; j < n; j++) {
      if (nums[i] + nums[j] === target && i !== j) {
        return [i, j]
      }
    }
  }
}

当然针对上述 for 循环优化部分，比如说让 j = i + 1 ，这样就可以有效避免重复数字的循环以及 i ≠ j 的判断。由于用到了两次循环，很显然时间复杂度为 O(n²)，并不高效。

哈希表​

我们不妨将每个数字通过 hash 表缓存起来，将值 nums[i] 作为 key，将 i 作为 value。由于题目的条件则是 x + y = target，也就是 target - x = y，这样判断的条件就可以由 nums[i]+ nums[j] === target 变为 map.has(target - nums[i]) 。如果 map 表中有 y 索引，那么显然 target - nums[i] = y，取出 y 的索引以及当前 i 索引就能够得到答案。代码如下

var twoSum = function (nums, target) {
  const map = new Map()

  for (let i = 0; i < nums.length; i++) {
    if (map.has(target - nums[i])) {
      return [map.get(target - nums[i]), i]
    }
    map.set(nums[i], i)
  }
}

而这样由于只有一次循环，时间复杂度为 O(N)。

双指针算法(特殊情况)​

假如理想情况下，题目所给定的 nums 是有序的情况，那么就可以考虑使用双指针解法。先说原理，假设给定的 nums 为 [2,3,5,6,8]，而目标的解为 9。在上面的做法中都是从索引 0 开始枚举，也就是 2,3,5…依次类推，如果没找到与 2 相加的元素则从 3 开始 3,5,6…依次类推。

此时我们不妨从最小的数和最大的数开始，在这个例子中也就是 2 和 8，很显然 2 + 8 > 9，说明什么？说明 8 和中间所有数都大于 9 即 3+8 ，5+8 肯定都大于 9，所以 8 的下标必然不是最终结果，那么我们就可以把 8 排除，从 [2,3,5,6] 中找出结果，同样的从最小和最大的数开始，2 + 6 < 9 ，这又说明什么？说明 2 和中间这些数相加肯定都下雨 9 即 2+3，2+5 肯定都小于 9，因此 2 也应该排除，然后从 [3,5,6] 中找出结果。就这样依次类推，直到找到最终两个数 3 + 6 = 9，返回 3 与 6 的下标即可。

由于此解法相当于有两个坐标(指针)不断地向中间移动，因此这种解法也叫双指针算法。当然，要使用该方式的前提是输入的数组有序，否则无法使用。

用代码的方式来实现：

  1. 定义两个坐标(指针)分别指向数组成员最左边与最右边，命名为 left 与 right。
  2. 使用 while 循环，循环条件为 left < right。
  3. 判断 nums[left] + nums[right] 与 target 的大小关系，如果相等则说明找到目标(答案)，如果大于则 右指针减 1 right—-，小于则左指针加 1 left++。
function twoSum(nums, target) {
  let left = 0
  let right = nums.length - 1

  while (left < right) {
    const sum = nums[left] + nums[right]
    if (sum === target) {
      return [left, right]
    }

    if (sum > target) {
      right--
    } else if (sum < target) {
      left++
    }
  }
}

针对上述两道算法题浅浅的做个分享，毕竟我还只是一名初入算法的小白。对我而言，我的算法刷题之旅还有很长的一段时间。且看样子这条路可能不会太平坦。

算法对我有用吗？​

在我刷算法之前，我在网上看到鼓吹算法无用论的人，也能看到学算法却不知如何应用的人。

这也不禁让我思考 🤔，算法对我所开发的应用是否真的有用呢？

在我的开发过程中，往往面临着各种功能需求，而通常情况下我会以尽可能快的速度去实现该功能，至于说这个功能耗时 1ms，还是 100 ms，并不在乎。因为对我来说，这种微小的速度变化并不会被感知到，或者说绝大多数情况下，处理的数据规模都处在 n = 1 的情况下，此时我们还会在意 n² 大还是 2ⁿ 大吗？

但如果说到了用户感知到卡顿的情况下，那么此时才会关注性能优化，否则，过度的优化可能会成为一种徒劳的努力。

或许正是因为我都没有用到算法解决实际问题的经历，所以很难说服自己算法对我的工作有多大帮助。但不可否认的是，算法对我当前而言是一种思维上的拓宽。让我意识到一道（实际）问题的解法通常不只有一种，如何规划设计出一个高效的解决方案才是值得我们思考的地方。

结语​

借 MIT 教授 Erik Demaine 的一句话

If you want to become a good programmer, you can spend 10 years programming, or spend 2 years programming and learning algorithms.

如果你想成为一名优秀的程序员，你可以花 10 年时间编程，或者花 2 年时间编程和学习算法。

这或许就是学习算法的真正意义。

参考文章​

初探动态规划

学习算法重要吗?

Loading Comments...
0%